В статье «О меновой закон без стоимости», опубликованной на сайте РУСО 8-го марта 2024 г. (см. https://polilog.ucoz.net/publ/menovoj_zakon_bez_stoimosti/1-1-0-59 ) рассматривается в качестве иллюстративного численного примера балансовая матрица «производства и потребления» на основе экономического способа производства некого условного капиталистического общества. Эта матрица описывает равновесное состояние для одного цикла (кругооборота) известного по К, Марксу воспроизводственного процесса действительной жизни общества: «Производство — Распределение – Обмен -Приобретение» (рис. 1, [2, с. 39]).
1.Балансовая матрица экономического способа производства
На рисунке 1 собственно балансовая матрица выделена тонированием соответствующих ячеек матричной таблицы.
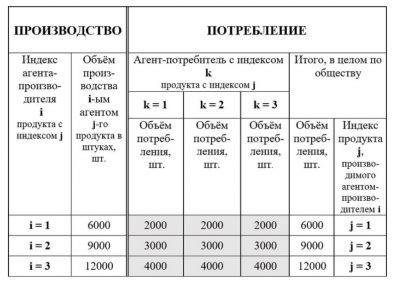
Рис. 1. Балансовая матрица «производство — потребление», описывающая равновесное состояние общества капитализма (при условии равенства структур производства и потребления по каждому агенту и равенства между собой самого воспроизводственного потребления этих агентов)
Как видно из схемы балансовой матрицы рисунка 1, это «условное общество» состоит из трёх агентов производителей (предприятий, коллективов или лиц) и, с другой стороны, — одновременно состоит из тех же трёх агентов, но уже в ранге потребителей (предприятий, коллективов, или лиц). При этом за один цикл воспроизводственного оборота первый агент-производитель (i = 1) производит 6000 единиц (шт.) продукции с индексом j = 1, второй агент-производитель (i = 2) производит 9000 единиц (шт.) продукции с индексом j = 2, третий агент-производитель (i = 3) производит 12000 единиц (шт.) продукции с индексом j = 3.
При этом за этот же цикл воспроизводственного оборота, но уже в части потребления произведённых продуктов, первый агент (i = 1) как агент-потребитель (k = 1) потребляет: 2000 единиц (шт.) продукции с индексом j = 1, 3000 единиц продукции с индексом j = 2 и 4000 единиц продукции с индексом j = 3. Это объём потребления представлен в столбце с индексом k = 1 таблицы рисунка 1.
Соответственно, см. балансовую матрицу рисунка 1, второй агент (i = 2) как агент-потребитель (k = 2) потребляет: 2000 единиц (шт.) продукции с индексом j = 1, 3000 единиц продукции с индексом j = 2 и 4000 единиц продукции с индексом j = 3. Это объём потребления представлен в столбце с индексом k = 2 таблицы рисунка 1.
Наконец, согласно балансовой матрице рисунка 1 третий агент (i = 3) как агент-потребитель (k = 3) потребляет: 2000 единиц (шт.) продукции с индексом j = 1, 3000 единиц продукции с индексом j = 2 и 4000 единиц продукции с индексом j = 3. Это объём потребления представлен в столбце с индексом k = 3 таблицы рисунка 1.
Для упрощения примера объемы потребления представленных в матрице рисунка 1 агентов-потребителей одинаковы как в объёмах, так и в структурах потребления. Более того, в целом для этого общества объемы и структура производства продукции та же, что и объёмы и структура потребления . Очевидно, что в потреблении агенты-потребители равны и каждый потребляет (получает) одно и то же количество продуктов по объёму каждого наименования. Далее, обозначим через Pik количество продукта в каждой ячейке матрицы, выделенной на рисунке 1 серым тонированием. Общепринято, что первый индекс указывает строку, а поэтому сохраним за первым индексом обозначение «i», то есть — обозначение агента-производителя (строка). Соответственно зададим обозначение второго индекса через «k» — обозначение агента-потребителя (столбец).
Рассмотрим собственно саму балансовую матрицу равновесного состояния, которая в таблице рисунка 1 выделена серым тонированием и отдельно представлена на рисунке 2. На схеме балансовой матрицы рисунка 2 [2, с. 40] объёмы продуктов вписаны с дополнительным указанием по каждому элементу условного обозначения соответствующего количества продукта в формате — Pik = ХХХХ.
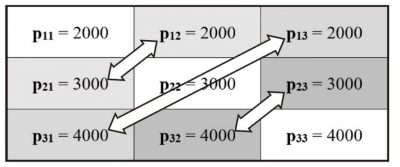
Рис. 2. Балансовая матрица «производство — потребление» экономического способа производства в условиях равновесного состояния «условного общества» капитализма
Дополнительно на рисунке 2 двухсторонними фигурными стрелками соединены те элементы (ячейки) балансовой матрицы, агенты которых, как агенты-производители, вовлечены в «обмен», на что указывает особое положение соответствующей ячейки матрицы и её пара индексов «i» и «k» при Pik. При этом наблюдается «зеркальное» отображение индексов этих пар ячеек, точнее, индексов соответствующих объёмов производства (i) и потребления (k) для указываемых двухсторонней стрелкой пар объемов (колтчеств) различных продуктов.
Например:
— левая короткая двухсторонняя стрелка (слева направо)
P21 = 3000 (i=2, k=1) и P12 = 2000 (i=1, k=2);
— средняя длинная двухсторонняя стрелка (слева направо)
P31 = 4000 (i=3, k=1) и P13 = 2000 (i=1, k=3);
— правая короткая двухсторонняя стрелка (слева направо)
P32 = 4000 (i=3, k=2) и P23 = 3000 (i=2, k=3);
Здесь «зеркальное отображение» двойных индексов представлено, образно говоря, тремя следующими их метаморфозами (>>> — знак метаморфозы зеркального отображения двойных индексов):
— левая короткая двухсторонняя стрелка (слева направо)
двойной индекс «21» (i=2, k=1) >>> «12» (i=1, k=2);
— средняя длинная двухсторонняя стрелка (слева направо)
двойной индекс «31» (i=3, k=1) >>> «13» (i=1, k=3);
— правая короткая двухсторонняя стрелка (слева направо)
двойной индекс «32» (i=3, k=2) >>> «23» (i=2, k=3).
Таким образом, каждый из агентов выступает одновременно и как агент-производитель (первый индекс двойной индексации — i), отчуждающий свой продукт, и как агент-потребитель (второй индекс двойной индексации — k), приобретающий для своего потребления продукт другого вида «взамен» отчуждённого продукта. В результате такого взаимодействия на основе экономического (капиталистического) способа производства осуществляется метаболический «обменный» процесс. Этот процесс, если типологии обеих продуктов есть «внешний предмет, вещь», принято именовать «товарообменом». Ячейки матрицы с элементами этих пар, дополнительно к двухсторонним стрелкам, выделены тонировкой различной интенсивности, одинаковой для каждой пары.
Так, например, пара элементов P12 = 2000 и P21 = 3000, соединённых малой двухсторонней фигурной стрелкой и имеющих светло-серое тонирование соответствующих ячеек балансовой матрицы (см. рис.2), последовательно читается следующим образом:
— Первый агент с индексом i = 1 отчуждает в пользу второго агента с индексом k = 2 ровно 2000 единиц (штук) произведённого им продукта с индексом j = 1, так как согласно матричной таблице рисунка 1 только первый агент производит продукты с индексом j = 1 (и только этот продукт). При этом второй агент с индексом i = 2 отчуждает в пользу первого агента k = 1 ровно 3000 единиц (штук) произведённого им продукта с индексом j = 2, так как согласно той же матричной таблице рисунка 1 только второй агент производит продукты с индексом j = 2 (и только этот продукт).
Следующая пара элементов P13 = 2000 и P31 = 4000, соединённых длинной двухсторонней фигурной стрелкой (см. рис. 2), последовательно читается следующим образом:
— Первый агент с индексом i = 1 отчуждает в пользу третьего агента с индексом k = 3 ровно 2000 единиц (штук) произведённого им продукта с индексом j = 1, так как согласно матричной таблице рисунка 1 только первый агент производит продукты с индексом j = 1 (и только этот продукт). При этом третий агент i = 3 агент отчуждает в пользу первого агента k = 1 4000 единиц (штук) произведённого им продукта с индексом j = 3, так как согласно матричной таблице рисунка 1 только третий агент производит продукты с индексом j = 3 (и только этот продукт).
Наконец, пара элементов P23 = 3000 и P32 = 4000, соединённых малой двухсторонней фигурной стрелкой и имеющих тёмное тонирование соответствующих ячеек балансовой матрицы (см. рис. 2), последовательно читается следующим образом:
— Второй агент с индексом i = 2 отчуждает в пользу третьего агента с индексом k = 3 3000 единиц (штук) произведённого им продукта с индексом j = 2, так как согласно матричной таблице рисунка 1 только второй агент производит продукты с индексом j = 2 (и только этот продукт). При этом третий агент i = 3 агент отчуждает в пользу второго агента k = 2 ровно 4000 единиц (штук) произведённого им продукта с индексом j = 3, так как согласно матричной таблицы рисунка 1 только третий агент производит продукты с индексом j = 3 (и только этот продукт).
В результате, — имеем три «меновых» отношения для всех трёх продуктов производимых и потребляемых в рассматриваемом иллюстративном примере условного общества.
Выполненный анализ условного примера формирования балансовой матрицы «производство — потребление» основан на учёте целостного единства воспроизводственного процесса действительной жизни общества, «единого целого» по К. Марксу. Выполненный анализ показывает, что так называемое «меновое отношение» возникает НЕ на базе «меновой стоимости товаров», которая как утверждает автор «Капитала», — «и есть их стоимость».
Описанный К. Марксом в «Капитале. Критика политической экономии» экономический (капиталистический) способ производства характеризуется в метатеории «Полилогия …» множеством категорий (понятий), основными из которых являются:
— базовый объект-предмет, а именно, – «внешний предмет, вещь», средства производства, товар;
— механизм взаимодействия агентов производства, а имннно, — «товарообмен (обмен), рынок;
— чистая эндогенная форма воспроизводства действительной жизни, а именно, — ЧЭФ «экономическая, капиталистическая»;
— отношения ограниченной частной собственности по поводу «средств производства»;
— и др.
Базой возникновения менового отношения, как показывает приведённый условный пример одного цикла кругооборота (обращения) воспроизводственного процесса, является устойчивое сохранение равновесного состояния общества как единого целого, что «свойственно всякому органическому целому», «всем общественным субстанциям». При этом заметим отсутствие в приведённом анализе экономического способа производства даже какого-либо упоминания стоимости.
Следовательно, можно полагать, утверждать, что полученные в приведённом примере меновые отношения есть выражение «органическим целым» общества его целостного единства. Это целостное единство сохраняется, тем более, и в социалистическом обществе, где доминирует уже не капиталистический способ производства, а доминирует функциональный способ производства.
2. Балансовая матрица функционального способа производства
Согласно метатеории «Полилогия современного мира …», как пишет её автор Шушарин А. С.:
— «… в функциональном производстве …
…чтобы понять отношения людей именно по поводу процессов, технологий, функций, ….
В первом рассмотрении диспозитивного среза функционального производства мы видим сеть функций соисполняемых, по образной формуле: они обеспечивают нас, а мы обеспечиваем других агентов, так что все обеспечивают всех.
Кроме конкретной, несопоставимой, стороны работы функция имеет и абстрактную сторону общественной формы своего бытия – положение функции, проявляющееся в относительном единообразии заключенного в ее выполнении уже абстрактного труда исполнителей функции. Положение функции – это ее своего рода общественное, производственное место, одномерный «вес», в соотнесении с другими («меновая стоимость»). В целом пока можно сказать так: вместо обмена, товара, потребительной стоимости и стоимости товара (в товарном производстве) в функциональном производстве соответственно выступают соисполнение, функция, работа и положение функции. Но если обмен товаров осуществляется на основе равенства (величин) их стоимостей, то соисполнение функций осуществляется логически радикально по-другому, на основе соответствия (величин) положения функций. Функциональность здесь и обнаруживает себя именно как связь соответствия (А.М. Магомедов).
Логика этого соответствия (по сравнению с логикой равенства), хоть в силу товарных стереотипов и необычна, но по сути проста. Функции, скажем, десяти проектировщиков завода, соответствует функция ста строителей корпуса этого завода, она соответствует функции двухсот монтажников оборудования, та и другая соответствуют функции пятидесяти транспортников, обеспечивающих стройку и подвоз оборудования. Очевидно, что величины десять, сто, двести, пятьдесят, как характеристики положения функций, никак не равны, но само соответствие положения функций при всякой данной эффективности труда различных работ есть отнюдь не менее точное соотношение, чем равенство … Основываясь на не менее жестких соответствиях функций, само функциональное производство в привычных «атомистических» формах не формализуется, начиная с логического «базиса».
В первом приближении соответствие функций оказалось связанным с абстрактным трудом, выраженным в виде некоторых обобщенных численностей коллективов» [3, с. 401 — 402].
И ещё: «В отличие от стоимости товара положение функции в ее первом превращении в количественную величину выступает как объем функции (величина положения), определяемый не величиной затрат абстрактного труда, а скоростью его затрат, мощностью. …
Объем функции имеет объективный смысл общественно необходимого расхода труда в его содержательной аналогии не с энергией, а с мощностью, т.е. с затратами энергии в единицу времени при выполнении данной функции…. Объем функции суть величина общественно-необходимого труда при его социальной равнонапряженности … Так что если узловой метафорой выражения особенности труда в товарной симметрии является равенство количества труда (в обменах), то в функциональной симметрии это – равенство напряженности труда (в соисполнении).
… В частности, логическое произведение объема функции на время ее выполнения оказывается «стоимостным» выражением выполнения этой функции, но в функциональном производстве действуют именно объемные, а не стоимостные отношения в соисполнении функций, так как «в чистом виде» обмена (выявляющего стоимость) здесь не существует» [3, с. 403].
Таким образом, функциональный (социалистический) способ производства характеризуется в метатеории «Полилогия …» множеством категорий (понятий), основными из которых являются:
— базовый объект-процесс, а именно, – «функция, социальная технология» или, проще, — работа;
— механизм взаимодействия агентов производства, а именно, — «соисполнение», план;
— чистая эндогенная форма воспроизводства действительной жизни, а именно, — ЧЭФ «функциональная, социалистическая»;
— отношения ограниченной иерархически группо-иерархической собственности по поводу «функций, работы»;
— и др.
Так как изложенный выше балансовый метод матричного анализа отношений является достаточно универсальным в действительной жизни общества, в анализе социального метаболизма современного общества, то далее рассмотрим в качестве иллюстративного численного примера простейшую балансовую матрицу «производства и потребления» на основе функционального способа производства некого условного социалистического общества. Эта матрица описывает равновесное состояние для одного цикла (кругооборота) воспроизводственного процесса действительной жизни общества «Производство — Распределение – Обмен — Приобретение» (рис. 3). Для упрощения восприятия примера объемы (мощности) функционального потребления представленных в матрице рисунка 3 агентов-потребителей одинаковы как в объёмах и мощности «потребления», так и в структурах функционального потребления. На рисунке 3 собственно балансовая матрица выделена тонированием соответствующих ячеек матричной таблицы.
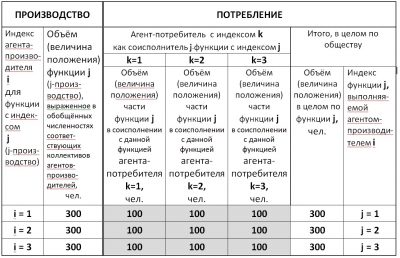
Рис. 3. Балансовая матрица «производство — потребление», описывающая равновесное состояние общества социализма (при условии равенства структур производства и потребления по каждому агенту и равенства между собой самого воспроизводственного потребления этих агентов)
Из представленных на рисунках 3 и 4 схем балансовой матрицы «Производство — Потребление», описывающих равновесное состояние общества социализма (при условии равенства структур производства и потребления по каждому агенту и равенства между собой самого воспроизводственного потребления этих агентов) имеем следующее.
Как видно из схемы рисунка 3, это «условное общество» социализма описывается тремя различными взаимоисполняемыми производственными функциями и состоит из трёх агентов производителей (предприятий или коллективов, или лиц) и, с другой стороны, — одновременно описывается тремя различными взаимоисполняемыми производственными функциями потребления и состоит из тех же трёх агентов, но уже в ранге потребителей (предприятий, коллективов, или лиц соисполнителей).
При этом за один цикл функционального воспроизводственного оборота (см. второй столбец таблицы рисунка 3):
— для выполнения первой функции (j = 1) первым агентом-производителем (i = 1) задействована мощность (объем функции) в 300 исполнителей (чел.) производственной функции с индексом j = 1;
— для выполнения второй функции (j = 2) вторым агентом-производителем (i = 2) задействована мощность (объем функции) в 300 исполнителей (чел.) производственной функции с индексом j = 2;
— для выполнения третьей функции (j = 3) третьим агентом-производителем (i = 3) задействована мощеность (объкм функции) в 300 исполнителей (чел.) производственной функции с индексом j = 3.
В тоже время, характеризуя этот же цикл воспроизводственного оборота, но уже в части соисполнения функции потребления, необходимо заметить следующее.
- Мощности (объем функции, величины положения функции) в 300 чел. первого агента (i = 1) как агент-производителя функции j = 1 распределены посредством функций соисполнения в потреблении мощностью по 100 чел. между тремя исходными функциями производственного потребления с индексами j = 1, j = 2 и j = 3 агентов-потребителей с индексами k = 1, k = 2 и k = 3. Это отображено в первой строке матрицы рис. 4 как:
300 = z11 + z12 + z13 = 100 + 100 +100 = 300.
Здесь объем (мощность) функции z11 = 100 агента k = 1 «соисполняется», можно сказать, сам с собой, то есть соисполняется с функцией агента k = 1. Эта замкнутость функции z11 = 100 самой на себя выделена на балансовой матрице рисунка 5 ячейкой с белым фоном без тонирования.
При этом, следует отметить, что объем (мощность) функции z12 = 100 агента-производителя k = 1, на что указывает первый индекс при z12, «соисполняется» (корреспондируется) в сочетании с функцией агента-потребителя k = 2, на что указывает второй индекс при z12.
Наконец, объем (мощность) функции z13 = 100 агента-производителя k = 1, на что указывает первый индекс при z13, «соисполняется» (корреспондируется) в сочетании с функцией агента-потребителя k = 3, на что указывает второй индекс при z13.
- Мощности (объем функции, величины положения функции) в 300 чел. второго агента (i = 2) как агент-производителя функции j = 2 распределены посредством функций соисполнения в потреблении мощностью по 100 чел. между тремя исходными функциями производственного потребления с инднесами j = 1, j = 2 и j = 3 агентов- потребителей с индексами k = 1, k = 2 и k = 3. Это отображено в второй строке матрицы рис. 4 как:
300 = z21 + z22 + z23 = 100 + 100 +100 = 300.
При этом, следует отметить, что объем (мощность) функции z21 = 100 агента-производителя k = 2, на что указывает первый индекс при z21, «соисполняется» (корреспондируется) в сочетании с функцией агента-потребителя k = 1, на что указывает второй индекс при z21.
Далее, объем (мощность) функции z22 = 100 агента k = 2 «соисполняется», можно сказать, сам с собой, то есть соисполняется с функцией агента k = 2. Эта замкнутость функции z22 = 100 самой на себя выделена на балансовой матрице рисунка 5 ячейкой с белым фоном без тонирования.
Наконец, объем (мощность) функции z23 = 100 агента-производителя k = 2, на что указывает первый индекс при z23, «соисполняется» (корреспондируется) в сочетании с функцией агента-потребителя k = 3, на что указывает второй индекс при z23.
- Мощности (объем функции, величина положения функции) в 300 чел. третьего агента (i = 3) как агент-производителя функции j = 3 распределены посредством функций соисполнения в потреблении мощностью по 100 чел. между тремя исходными функциями производственного потребления с индексами j = 1, j = 2 и j = 3 агентов-потребителей с индексами k = 1, k = 2 и k = 3. Это отображено в третьей строке матрицы рис. 4 как:
300 = z31 + z32 + z33 = 100 + 100 +100 = 300.
При этом, следует отметить, что объем (мощность) функции z31 = 100 агента-производителя k = 3, на что указывает первый индекс при z31, «соисполняется» (корреспондируется) в сочетании с функцией агента-потребителя k = 1, на что указывает второй индекс при z31.
Далее, объем (мощность) функции z32 = 100 агента-производителя k = 3, на что указывает первый индекс при z32, «соисполняется» (корреспондируется) в сочетании с функцией агента-потребителя k = 2, на что указывает второй индекс при z32.
Наконец, объем (мощность) функции z33 = 100 агента k = 3 «соисполняется», можно сказать, сам с собой, то есть соисполняется с функцией агента k = 3. Эта замкнутость функции z33 = 100 самой на себя выделена на балансовой матрице рисунка 5 ячейкой с белым фоном без тонирования.
Для упрощения восприятия примера объемы (мощности, величины положения) функций потребления в соисполнении представлены в матрице рисунков 4 и 5 агентов-потребителей одинаковы как в объёмах, так и в структурах потребления. Более того, в целом для этого общества объемы и структура функций в производстве та же, что и объёмы и структура функций в потреблении. В данном примере в функциях потребления агенты-потребители равны и каждому в соисполнении соответствует оино и то же объём функции в человеках по каждому наименованию сопряжённой функции. Эти объёмы (мощности) функций обозначены через zik по каждой ячейке матрицы и выделены на рисунках 3 и 4 серым тонированием. Общепринято, что первый индекс указывает строку, а поэтому сохраним за первым индексом обозначение «i», то есть — обозначение агента-производителя функции (строка). Соответственно зададим обозначение второго индекса через «k» — обозначение агента-потребителя соисполнения функции (столбец).
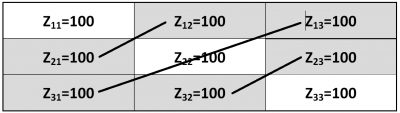
Рис. 4. Балансовая матрица «производство — потребление» в условиях равновесного состояния «условного общества» социализма
Дополнительно на рисунке 4 отрезками прямых линий ( как двухсторонними фигурными стрелками) соединены те элементы (ячейки) балансовой матрицы, функции которых находятся в соответствии и соисполнении. При этом их агенты-соисполнители, их численность, составляют величину мощности (объём и величину положения) соответствующих функций и обеспечивают их «точное соотношение» и «жёсткое соответствие функций». На эту вовлеченность в «жёсткое соответствие функций» указывает особое положение соответствующей ячейки матрицы и её пара индексов «i» и «k» при zik. При этом наблюдается «зеркальное» отображение индексов этих пар ячеек, точнее, индексов соответствующих объёмов (мощностей) функций в части производства (i) и потребления (k) для указываемых отрезками прямых линий пар объемов (мощностей, величин положения) функций — zik = ХХХ, например:
— левый короткий отрезок прямой (слева направо)
Z21 = 100 (i=2, k=1) и Z12 = 100 (i=1, k=2);
— средний отрезок прямой (слева направо)
Z31 = 100 (i=3, k=1) и Z13 = 100 (i=1, k=3);
— правый отрезок прямой (слева направо)
Z32 = 100 (i=3, k=2) и Z23 = 100 (i=2, k=3).
Здесь «зеркальное отображение» двойных индексов как «жёсткое» соответствие соисполняемых функций представлено, образно говоря, тремя следующими их метаморфозами (>>> — знак метаморфозы зеркального отображения двойных индексов):
— левый короткий отрезок прямой (слева направо)
двойной индекс «21» (i=2, k=1) >>> «12» (i=1, k=2);
— средний отрезок прямой (слева направо)
двойной индекс «31» (i=3, k=1) >>> «13» (i=1, k=3);
— правый короткий отрезок прямой (слева направо)
двойной индекс «32» (i=3, k=2) >>> «23» (i=2, k=3).
В этой связи уместно напомнить следующий момент из метатеории «Полилогия современного мира …»:
— «… в первом рассмотрении диспозитивного среза функционального производства мы видим сеть функций соисполняемых, по образной формуле: они обеспечивают нас, а мы обеспечиваем других агентов, так что все обеспечивают всех» [3, c. 401].
Таким образом, каждый из агентов выступает одновременно и как агент-производитель функции (первый индекс двойной индексации — i), то есть, — «обеспечивающий нас», и как агент-потребитель (второй индекс двойной индексации — k), то есть, — «мы обеспечиваем других агентов». В результате, — «»все обеспечивают всех».
В итоге такого взаимодействия на основе функционального (социалистического) способа производства осуществляется социальный метаболизм «работ», то есть разнообразных функций действительной жизни общества. Этот функциональный метаболизм доминирует в социалистическом обществе на основе функционального способа производства. Ячейки матрицы с элементами этих пар выделены на рисунке 4 тонировкой различной интенсивности, одинаковой для каждой пары.
Так, например, пара элементов Z12 = 100 и Z 21 = 100, соединённых малым отрезком прямой и имеющих светло серое тонирование соответствующих ячеек балансовой матрицы (см. рис.4), последовательно читается следующим образом:
— Первый агент с индексом i = 1 выполняет, соисполняет, свою функцию j =1 мощностью в 100 чел. в пользу второго агента с индексом k = 2. В свою очередь второй агент с индексом i = 2 выполняет, соисполняет, свою функцию j =2 мощностью в 100 чел. в пользу агента с индексом k = 1.
Следующая пара элементов Z13 = 100 и Z31 = 100, соединённых длинным отрезком прямой (см. рис. 4), последовательно читается следующим образом:
— Первый агент с индексом i = 1 выполняет, соисполняет, свою функцию j =3 мощностью в 100 чел. в пользу третьего агента с индексом k = 3. В свою очередь третий агент с индексом i = 3 выполняет, соисполняет, свою функцию j =3 мощностью в 100 чел. в пользу агента с индексом k = 1.
Наконец, пара элементов Z23 = 100 и Z32 = 100, соединённых малым отрезком прямой и имеющих тёмное тонирование соответствующих ячеек балансовой матрицы (см. рис. 4), последовательно читается следующим образом:
— Второй агент с индексом i = 2 выполняет, соисполняет, свою функцию j =2 мощностью в 100 чел. в пользу третьего агента с индексом k = 3. В свою очередь третий агент с индексом i = 3 выполняет, соисполняет, свою функцию j =3 мощностью в 100 чел. в пользу агента с индексом k = 2.
В результате, — имеем три пары соисполняемых функций, «жёстких соответствий функций» и «точных соотношений», всех трёх производственных функций и их же «потребляемых» в рассматриваемом иллюстративном примере условного общества социализма на основе функционального способа производства.
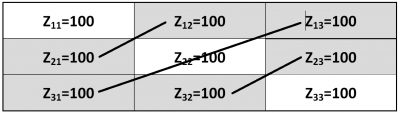
Рис. 4 (повторно). Балансовая матрица «производство — потребление» в условиях равновесного состояния «условного общества» социализма
3.Балансовая матрица индустриального метода производства
В заключение приведем подобный пример, но уже индустриального общества, общества с одномоментной реализацией двух вышеописанных примеров способа производства. За основу возьмем балансовую матрицу «капитализма» рис. 1 и 2, а так же часть балансовой матрицы «социализма» рис. 3 и 4. При этом будем считать, что j—производство j = 3 агента производства i = 3 на 50 % основывается на экономическом (капиталистическом) способе производства, а другие 50 % основывается на функциональном (социалистическом) способе производства. Соответствующая балансовая матрица представлена на рисунке 5.
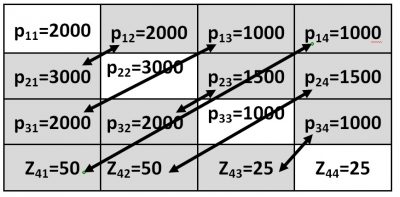
Рис. 5. Балансовая матрица «производство — потребление» в условиях равновесного состояния «условного общества» на базе одновременной совместной реализации экономического (капиталистического) (pxx =…) и функционального (социалистического) (z4x =…, агент k=4 ) способов производства
Понятно, что теперь вместо одного агента-производителя с индексом i = 3 и одного агента-потребителя k=3, получим двух агентов-производителей i = 3 и i = 4 и двух агентов-потребителей k=3 и k=4 (см. рис. 5).
Как видно из балансовой матрицы рисунка 5 в индустриальном обществе вполне допустима одновременная реализация двух способов производства, экономического и функционального, лежащих в основе двух различных социально-воспроизводственных градаций, — социализма и капитализма.

